In modern algebra we are used to deal with quantities in the form of numbers. We are given the number 3 or 5.61 and then we work with them.
In Euclid's geometry we deal with quantities as straight segments drawn with a straight edge, which is a ruler without the markings.
We don't need to know if a given segment has length 12.3 cm or 7.43 mm. We just deal with these segments as given entities.
The first exercise that Euclid teaches us is, given a segment, to build a triangle in which all its three sides are equal, and each with the length of our given segment. Such a triangle is called equilateral.
But first of all, we are given the segment, coloured in blue:
We could have shown the segment naked, without marking its points or even without labels. It depends on whether you rely more on visuals or on text.
Now we take the compass and describe a red circle with centre in A and radius AB, and a green circle with centre in B and radius BA:
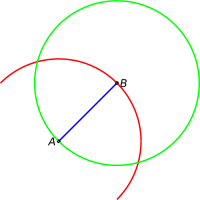
Notice how the two circles have two points of intersection. We can choose the one that we wish.
Also, there is no need to draw the whole circles! Just draw arcs as small as you can to keep the drawing clean:
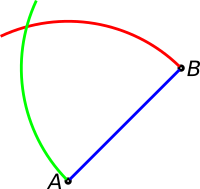
In fact, we could have drawn the arcs even smaller here, but we want to remark the point from which the circle begins.
Let's now redraw these arcs in grey colour and in dashed style, so that we can remark what is important: the intersection point C:

Finally, we just need to draw the segments AC and BC to get our equilateral triangle:

All points in the red circle are at a distance AB from A.
All points in the green circle are at a distance BA from B.
The intersection point C is at distance AB from A and BA from B, but AB = BA.
Then, AB = BC = AC, and the three sides are equal.
[GCLC file]