As in algebra, we may be given two numbers to be added or subtracted. But these numbers are here in the form of segments, so in order to add or subtract them we need to be able to concatenate one after the other.
In other words, if we are given a segment AB and a point P, we must be able to transport the segment AB to the point P without altering the length AB. We have two choices: either to place point A at P or to place point B at P, depending on our needs.
Our initial setup is this, then: a given segment AB to be transported and a fixed point P where we will anchor point B (or A, but we arbitrarily choose B).

The next step is to draw a segment connecting the two points that we want to connect. In this case, we want to transport point B to P, so we draw this connection.

Now we will understand why Euclid taught us to build equilateral triangles before. What we need now is to build an equilateral triangle from the connecting (dashed grey) segment. We must apply all the steps of the previous proposition, with the following result:
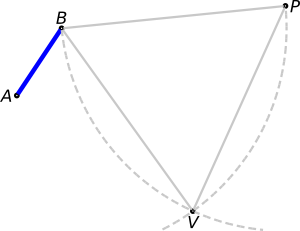
We have drawn the complete equilateral triangle in solid grey now. Pay attention to point V, which will be our pivotal vertext.
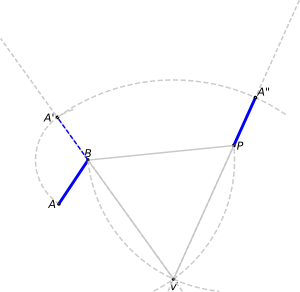
We will now turn our original blue segment wrt B, so that we can *align* it along the direction VB. For this, we first *produce* (extend) the line dictated by VB. Then we pin the compass at B and draw a circle from A to the latter line. Where the circle cuts the line, point A', we have a blue segment with the same length than AB. We have increased the line width of AB to remark that this is our original segment.

The next step is quite obvious: we need to pivot the whole segment VA' with respect to V, so we pin the compass at V and start drawing at A', and we need to stop when intersecting with the line produced from VP, which determines point A".

It is clear now that PA" = AB, because VB = VP and VA' = VA". We can draw in blue the final segment, to remark it has the same length as the original.
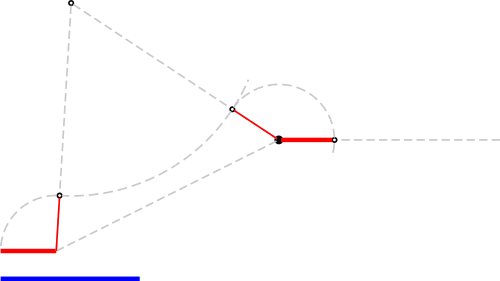
We are given two segments, a red one and a blue one. (Here we will not deal with labels for points.) And we are asked to sum them and give the result from a given black point somewhere along the grey line. The grey line here just means that we want the result expressed along the horizontal direction.

We first choose to transport the red segment to the black point. For this, we need the method of proposition 2. First we connect one extreme of the red segment to our black point, and build an equilateral triangle out of it. Then we align our red segment to one of the sides of the triangle. Notice how here we turn the segment inwards instead of outwards as before, but the process is the same, and the resulting figure is cleaner. Then we pivot the arm containing the red segment so that it is transported to the black point. Finally, since we are asked to express our result along the horizontal, we rotate the segment along this direction:
The next step is to do the same for the blue segment, but now, instead of transporting such segment to the black point, we do transport it to the point in which the transported red segment ends. Again, we connect one extreme of the blue segment to the point where we want to transport it, we build the equilateral triangle, we align the segment with one of its sides (inwards again), we pivot the arm and finally we rotate the segment along the horizontal direction.
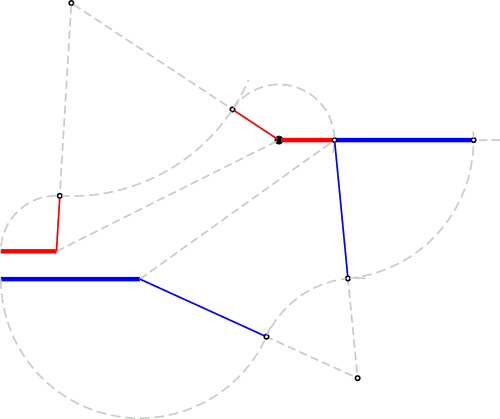
In the image above we see the sum of both segments. It is equivalent to an algebraic sum, but disregarding numbers and focusing on lengths. Notice how we don't need to measure with a ruler or with a rigid compass!
We could add more segments now and all of them could be added to the sum.
[GCLC file]