Here we limit ourselves to subtract the biggest from the smallest. Working with real lengths it is not meaningful to deal with a negative quantity.
If we are given two segments and we want to subtract them, we first need to transport one of them to one of the endpoints of the other.
Imagine that both segments (one blue and another red) already have a common endpoint, since we have already practised the transport in the previous proposition.
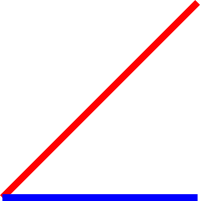
Then we just take the smallest (blue) segment and describe a circle with its length (with centre at the common endpoint). In fact, it is enough to describe the arc that cuts the biggest segment:
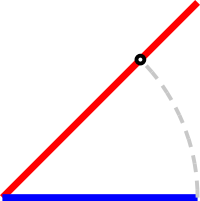
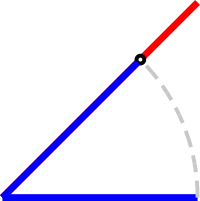
Finally, we paint in blue what corresponds to the length of the smallest segment, so that the remaining red piece is the result of the subtraction.
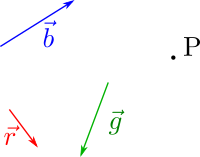
I don't like when we deal with mathematics as if we could separate its topics in a perfect classification. All topics are related, and here, vectors are ideal to understand what we are doing with addition and subtraction.
Suppose we want to add vectors |r>, |g> and |b>, which are red, green and blue, respectively. And we want to express our result as a final vector sum in point P. Our initial setup is, then,
The order in which we add is not important, so let's choose to add first |r>, then |g> and then |b>.
First we transport |r> to the point P with the method we already know. If we call the endpoints of a vector 'tail' 'tip', what we need is to place the tail of |r> at P:
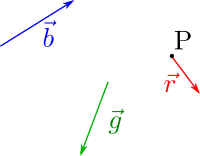
Next step consists in placing the tail of |g> at the tip of |r>. When adding vectors, we are just building a chain in whicht he tail of the next is attached to the tip of the previous.
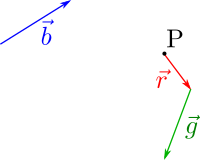
Now we do the same for the blue vector and get:

The final step is to build the sum vector, which goes from the first tail to the last tip. We draw the sum vector in magenta:
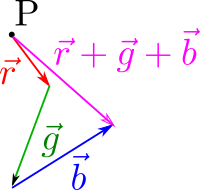
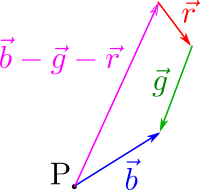
Imagine now that we depart from the same initial setup but now we want to perform |b> + |r> - |g>.
The first thing we need to know is that by doing |a> ---> -|a>, that is, by changing the sign of a whole vector, what we are doing, graphically speaking, is to exchange tail and tip.
So notice how we can rewrite |b> + |r> - |g> as |b> + |r> + (-|g>).
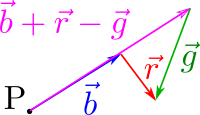
We can draw other variants, for example
In the context of Euclid's books, we are just adding and subtracting scalars, not vectors, so it is important that we have all the arrows along the same direction. We choose for these drawings an arbitrariy direction, to illustrate the point that any direction is valid.
Given a direction, we must (arbitrarily) define a positive number as an arrow parallel to the direction and a negative number when it is anti-parallel to it.
We begin by adding having the numbers r, g, and b, a point P in which to attach the result, and an arbitrary direction. Notice that all numbers must be parallel to that direction.
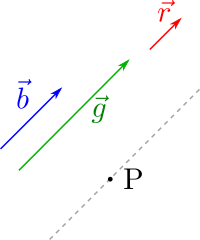
Here, positive is defined as North-East and negative as South-West. Then, all three numbers b, g and r are positive.
So now we add these arrows (b + g + r) and obtain:
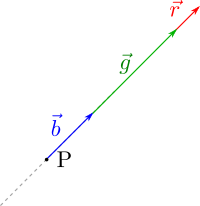
In the picture above we still write the labels as vectors, but from now on we will write them as scalars.
Notice this is what we did in the previous proposition, although here we don't show the actual process.
We can also subtract by applying the same vector philosophy.
For b - g + r we see how the green arrow is connected from tip to tail, which is the way of subtraction. Notice how the final result, in magenta, is negative, because it points South-West.
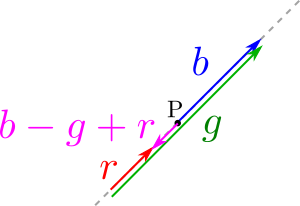
Don't get confused by the typical mess of being able to subtract a positive number or to add a negative number. Both have a different graphical interpretation. In the previous figure, the green arrow is a positive number being subtracted. We would have obtained the same result by having the antiparallel version of g, pointing South-West, and then *adding* it, connecting first its tail. A similar thing would happen if instead of adding a positive number you decide to subtract a negative number. We would have a different picture with the same result.
Conclusion: thinking Euclid's addition and subtraction in vector terms is very useful. Moreover, when drawing vectors with paper and pencil, it is very useful to get a compass and use Euclid's methods to transport these vectors!