A triangle in which two sides are equal (red) and the third is not equal (black) is called isosceles.
Let's explore now some angular properties of this triangle.

We begin by producing (extending) the equal sides, but now with an infinite line. Instead, we produce only an additional segment on each side, of arbitrary length, and we use the compass to ensure that both productions are equal in length (and in colour, yellow).
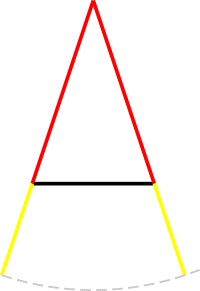
Now we connect in blue the following segments and we explicitly draw the angle common to both equal sides:
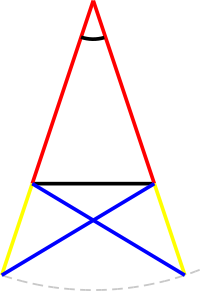
Here we need to do the mental exercise to imagine the last figure as the superposition of the two next figures:
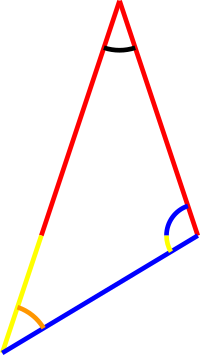
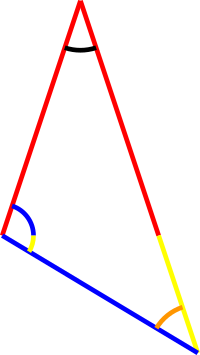
These two triangles are clearly similar (and congruent).
Here we have a single black angle, two yellow angles, two orange angles and two blue angles. Of course, equal colour must mean equal value of the angle, but this is what we want to show.
The blue angles are the internal angles of the original triangle at its base.
First, since our last two figures are congruent, the orange angles must be the same.
Also, the sum of the blue + yellow angles is also the same in both figures.
Now we can extract two triangles from the main figure that are also congruent:

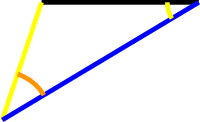
From this figure we deduce that the two yellow angles are equal.
Then, the two orange angles are also equal.
I have never seen the real point in this proposition. To me, one could summon a principle of symmetry to define the isosceles triangle and then all constructions in one side would be symmetric to the constructions on their other side.
What I like, though, is how by producing segments we can create new triangles that can gives us some transitivity. Transitivity means having two systems with one element in common and using it to establish a new system formed by the two non-common elements. In this case, the black angle serves as such a pivot.
Finally, we can show the complete figure, where equal color always mean equal value:
