We call motion in one dimension that motion with a single degree of freedom. We could establish its Lagrangian, either with generalised or with Cartesian coordinates, and then, once we have the equations of motion, we could integrate them.
There is another valid path. We establish the expression for the (conserved) energy
E = (m/2)ẋ² + U(x) .
Then, since ẋ=dx/dt, we can isolate dt as
dt = dx·(m / (2[E-U])¹⸍² = (m/2)¹⸍² · 1/(E-U(x))¹⸍².
We integrate to obtain
t = (m/2)¹⸍² + ∫ dx / (E-U(x))¹⸍² + C.
There are two constants to be determined in this integral: E and C.
Since T > 0, then E = T + U > U and E - U = T > 0. So the square root is always real. This means that motion must be confined to those places where U(x) < E. The energy E acts as a ceiling for U(x), or as upper bound. Consider the function U(x) of the figure:
U(x)
|
|
| ,-'-.
| ,' \
.__ | / \
``-..| / \
|`-._ / |
________|____ A_______________________B_____________C______U=E
| |`. /| |
| | \ / | |·
| | \ / | |·
| | \ / | |.
| | \ / | | \
| | \ / | | \
| | `. ,' | | `.
| | `-..,' | | `.
| | | | `.
| | | | `.
''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''' x
x₁ x₂ x₃
In this figure we have a curve U(x) and a horizontal line U=E. Motion is only possible for regions that are below this horizontal line. This means that the region to the left of A is forbidden, and so is the region between B and C.
Allowed regions are the one between A and B and the region to the right of C.
The points A, B and C are called *turning points* and are points for which U(x)=E. They are the limits of motion for an allowed region, and mathematically they make the denominator 0.
When a region is bounded by two points, motion takes place in a spatially bounded or finite region. For example, the region between A and B corresponds to a finite motion between x₁=A and x₂=B. A particle there will display oscillatory motion, going back and forth between x₁=A and x₂=B. See how between these two points we have a potential well.
When a region, like that to the right of C, is bounded by a single turning point, then motion is infinite and the particle goes to infinity.
For the oscillatory case between A and B we can integrate the period of oscillation T, which is the time to go from x₁ to x₂ and back to x₁. Since motion is reversible, it is clear that the time to go from x₁ to x₂ is the same as the time to go back. Then, we just calculate the time from x₁ to x₂ and multiply by 2 to get T,
t = (m/2)¹⸍² + ∫{x;x₁;x₂} dx / (E-U(x))¹⸍² + C.
Determine T of a simple pendulum (mass m suspended by a massless string of length l in a uniform gravitational potential with acceleration g) as a function of the amplitude of the oscillations.
In other words, we need to integrate t. For a simple pendulum, we use polar coordinates
E = (m/2)l²[ϕ·]² - mglcosϕ ,
where ϕ is our polar angle, taken wrt the vertical, and where U=0 is defined when the pendulum is horizontal, or ϕ=±π/2. We don't need the pendulum to reach such angle, we just use this case for the definition of U=0. In fact, we define the maximum ϕ as ϕ₀.
Since E is constant, we can choose a particular state, like ϕ=ϕ₀, in which kinetic energy is clearly 0, and then E = -mglcosϕ₀. Then
E = (m/2)l²[ϕ·]² - mglcosϕ = -mglcosϕ₀.
See how this motion is in one dimension, ϕ, and how +ϕ₀ and -ϕ₀ are the turning points in an allowed region. So motion will be going back and forth between these two points.
We could calculate the time to go from -ϕ₀ to ϕ₀ and multiply by 2, but since motion is symmetric (because the potential is), we can calculate the time from ϕ=0 to ϕ₁ and multiply by 4.
The integral now is along ϕ instead of x, because ϕ is our only dof,
T = 4(ml²/2)¹⸍²·∫{ϕ;0;ϕ₀} dϕ / (-mglcosϕ₀+mglcosϕ)¹⸍².
We can rearrange this to get
T = 4(l/(2g))¹⸍²·∫{ϕ;0;ϕ₀} dϕ / (-cosϕ₀+cosϕ)¹⸍².
In the denominator, inside the square root, we have two linear terms subtracting. But for integrals, it is more convenient to have the subtraction of two square terms.
Since cosϕ = 1 - 2sin²(ϕ/2), then cosϕ-cosϕ₀ = 2(sin²(ϕ₀/2) - sin²(ϕ/2)), and now we have what we wanted. We rewrite our integral as
T = 2(l/g)¹⸍²·∫{ϕ;0;ϕ₀} dϕ / (sin²(ϕ₀/2)-sin²(ϕ/2))¹⸍².
The latter modification was done in order to approach a denominator of the form (1 - (something)²)¹⸍², which is the ideal form for a square root in the denominator of an integral. For this, we can make another substitution,
sinξ = sin(ϕ/2) / sin(ϕ₀/2).
When we do a change of variables in an integral, we need to see how the differential change as well. For this, we perform the total derivative on the latter expression,
dξcosξ = (dϕ/2)·cos(ϕ/2) / sin(ϕ₀/2).
But what we want is dϕ alone, in order to plug the result in the integral, so
dϕ = 2dξ·sin(ϕ₀/2) · cosξ / cos(ϕ/2).
But this is not valid yet, since our result must only contain the new variables. This means that cos(ϕ/2) cannot be there as such. We can use again the initial expression for the substitution of variables to see that
cos(ϕ/2) = (1 - sin²ξ·sin²(ϕ₀/2))¹⸍².
Our differential becomes
dϕ = 2dξ·sin(ϕ₀/2) · cosξ / (1 - sin²ξ·sin²(ϕ₀/2))¹⸍².
Then, our integral becomes a bit messy, but many terms cancel. For changes of variables, we also need to take the limits of integration into account. For ϕ they were {0;ϕ₀}. See how for ϕ=0 we get ξ=0 and for ϕ=ϕ₀ we get ξ=π/2. Then,
T = 4(l/g)¹⸍²∫{ξ;0;π/2}·dξ / (1 - sin²(ϕ₀/2)·sin²ξ)¹⸍².
From elliptic integral theory, we know that the complete elliptic integral of the first kind, K(k), is
K(k) = ∫{ξ;0;π/2}·dξ / (1 - k²·sin²ξ)¹⸍².
So our period is
T = 4(l/g)¹⸍²·K(k=sin(ϕ₀/2)).
There are no (known) analytical solutions for them. We can express the integral as a power series which, to second order of k, is
K(k) ≃ (π/2)·( 1 + k²/2²).
Then, our period is approximated as
T ≃ 2π(l/g)¹⸍²·(1 + (1/4)·sin²(ϕ₀/2)).
For small angle ϕ₀ we expand sin(ϕ₀/2) as ϕ₀/2, and then its square as ϕ₀²/4. Then,
T ≃ 2π(l/g)¹⸍²·(1 + ϕ₀²/16)).
The order 0 is the usual expression for very small oscillations, which does not depend on the amplitude.
With this approach, we could obtain T to any precision we want, by using more and more terms in the series. Compare the power of this method with other approaches that only allow you to get the 0 order term!
Determine the period of oscillation, as a function of the energy, when a particle of mass m moves in fields for which the potential energy is
a) U = A|xⁿ]
We need to integrate between x=0 and xmax. What is the value of xmax? Since at the turning point we get zero kinetic energy, at that point we have E=-U=-A[xⁿ|. For this limit we don't care about the sign of x, due to symmetry of the potential, so E/A = xⁿ and then xmax = (E/A)¹⸍ⁿ. In the integral we don't care about the sign either, since the positive or the negative part of the oscillation must contribute equally to the period,
T = 2(2m)¹⸍²·∫{x;0;xmax} dx / (E - Axⁿ)¹⸍².
Again we have an integral with a square root as denominator. We want this denominator to be as (1-yⁿ)¹⸍². This needs the transformation Axⁿ/E = yⁿ. Performing the total derivative on this expression we get
nyⁿ⁻¹dy=(A/E)nxⁿ⁻¹ yⁿ⁻¹ = (A/E)¹⁻¹⸍ⁿ·xⁿ⁻¹ dx = (A/E)⁻¹⸍ⁿ·dy.
The integral becomes
T = 2(2m/E)¹⸍²·(E/A)¹⸍ⁿ·∫{y;0;ymax} dy / (1 - yⁿ)¹⸍²,
where ymax = (A/E)xmaxⁿ = (A/E)·(E/A)=1.
The integral is not yet workable. It is a matter of experience to see that it can be converted into a beta function B(a,b), defined as
B(a,b) = ∫{u;0;1} uᵃ⁻¹(1-u)ᵇ⁻¹du.
In order to achieve this we perform the change yⁿ=u. Then, we again need the total differential of this expression,
nyⁿ⁻¹dy=du dy = du / (n·u¹⁻¹⸍ⁿ).
Considering only the previous integral (without prefactors), and adapting the limits of integration, which are again 0 and 1, we get
∫{y;0;1}dy/(1-yⁿ)¹⸍² = ∫{u;0;1}·du / (n·u¹⁻¹⸍ⁿ·[1-u]¹⸍²) =
= (1/n)·∫{u;0;1}u¹⸍ⁿ⁻¹·(1-u)⁻¹⸍²·du.
Here we already recognise the beta function with a=1/n and b=1/2. The next step is to recall how the beta function is related to the gamma function Γ,
B(a,b) = Γ(a)·Γ(b) / Γ(a+b) = Γ(1/n)·Γ(1/2) / Γ(1/2+1/n).
We use here Euler's reflection formula
Γ(1-z)Γ(z) = π / sin(πz)
to plug z=1/2 and get
Γ(1/2) = (π)¹⸍².
With all this, our integral, including prefactors, becomes
T = (2/n)·(2πm/E)¹⸍²·(E/A)¹⸍ⁿ·Γ(1/n) / Γ(1/2+1/n).
This is the exact expression for the period as a function of E.
Could we have guessed that T goes as E¹⸍ⁿ⁻¹⸍² by mechanical similarity? We know that (t'/t) goes as (l'/l)¹⁻ⁿ⸍², and we also know that E'/E = (l'/l)ⁿ, so (t'/t) = (E'/E)¹⸍ⁿ⁻¹⸍², which is what we got. Again we see how powerful is to use mechanical similarity.
b) U = -U₀/cosh²(αx) with -U₀ < E < 0.
In this case, the function U(x) is not homogeneous, so we cannot guess the functionality with mechanical similarity.
We have to determine the limits of integration. In fact, we only have to determine the energy for which we have a turning point, so we need E=U (setting kinetic=0), and then E=-U₀/cosh²(αx), which leads to cosh(αx) = (U₀/|E|)¹⸍² and finally, we have
xmax = (1/α)·arcosh[(U₀/|E|)¹⸍²].
Our integral becomes
T = 2(2m)¹⸍²·∫{x;0;xmax}dx / (E + U₀/cosh²(αx))¹⸍².
Let's try to develop the integral. We omit the prefactors for now, and we write b as shorthand for (|E|/U₀)¹⸍², so we get
∫dx/(E+U₀cosh²(αx))¹⸍² = ∫cosh(αx)·dx/(U₀+Ecosh²(αx))¹⸍² = = 1/√|E|·∫bcosh(αx)·dx / ( 1 - b²cosh²(αx))¹⸍² = = 1/√|E|·∫ y·dx / (1 - y²)¹⸍²,
where y = b·cosh(αx). But then we need to perform the total derivative on this transformation and get
dx = dy / (iα) / (b²-y²)¹⸍².
The integral becomes
( 1 / (iα√|E|) ) · ∫ y·dy / [ (1 - y²)¹⸍² (b²-y²)¹⸍² ].
Let's focus on this integral:
∫ y·dy / [ (1 - y²)¹⸍² (b²-y²)¹⸍² ].
It does not seem a pleasant function to integrate, but when we have two multiplying entities in the denominator we can do the following trick. Let's assume D and d to be our two entities at the denominator. Then
1/(D·d) = (D+d) / [(D·d)·(D+d)] = *
No surprises here, just multiplying by 1. But then,
* = ( 1/d + 1/D ) / (D + d).
Why bothering with such a complication? Notice how we obtain an expression that can be integrated.
Our integral becomes
( y/(1-y²)¹⸍² + y/(b²-y²)¹⸍² ) / ((1-y²)¹⸍² + (b²-y²)¹⸍²) = = -ln[ (1-y²)¹⸍² + (b²-y²)¹⸍² ].
Adapting the limits of integration to y we see that we integrate from y=1 to y=b. Then we get
-ln[ (1-y²)¹⸍² + (b²-y²)¹⸍² ] |{y;1;b} =
= -ln[(1-b²)¹⸍²] + ln[(b²-1)¹⸍²] =
= ln[(b²-1)¹⸍²/(1-b²)¹⸍²] =
= ln(-i) = -iπ/2.
Collecting all lost prefactors,
T = 2(2m)¹⸍² / (iα√|E|) · (-iπ/2) = -(π/α)(2m/|E|)¹⸍²,
where we don't care about the sign, and we can drop it.
c
c) U = U₀tan²(αx)
Our integral is
T = 2(2m)¹⸍²·∫{x;0;xmax}dx / (E - U₀tan²(αx))¹⸍².
We get xmax by doing E=U, so xmax = (1/α)·arctan((E/U₀)¹⸍²).
We define b=(U₀/E)¹⸍², and the integral becomes
2(2m/E)¹⸍²∫dx/(1-b²tan²(αx))¹⸍².
Now we change b·tan(αx) by sinξ, and the total differential provides
αbdx / cos²(αx) = cosξ·dξ dx = cosξcos²(αx)·dξ / (αb) dx = cosξ·dξ / [ αb · (1+tan²(αx)) ] dx = b·cosξ·dξ / [ α· (b²+b²tan²(αx)) ] dx = b·cosξ·dξ / [ α· (b²+sin²ξ) ].
The integral becomes
(2b/α)·(2m/E)¹⸍²∫dξ / (b²+sin²ξ) = (2/(αb))·(2m/E)¹⸍²∫dξ / (1+sin²ξ/b²).
We now have the task to face the integral
∫dξ / (1+sin²ξ/b²) = ∫dξ b²/ (b²+sin²ξ)..
This integral smells like arctan, since we know that
(d/dx)arctan(u(x)) = (du/dx) / (1+u²).
Let's perform a trick:
b²/(b²+sin²ξ) = b²/(b²cos²ξ+b²sin²ξ+sin²ξ) = *
This move seems quite innocent, but see how it develops
* = b²/(b²cos²ξ + (1+b²)sin²ξ) = = 1 / (cos²ξ + sin²ξ·(1+b²)/b²) = = 1 / (cos²ξ + cos²ξ·tan²ξ·(1+b²)/b²) = = (1/cos²ξ) / (1 + tan²ξ/tan²y) =
where we define tany=b/(1+b²)¹⸍². Take into account here that 1/cos²ξ is the derivative (d/dx)tanξ, so
= tany·(d/dx)[tanξ/tany] / (1 + tan²ξ/tan²y)= *
And now this is exactly the derivative of the arctan of...
* = tany·(d/dx)arctan[tanξ/tany].
If we take into account that the limits of integration are ξ=0 and sinξ = 1, which implies tanξ → ∞, we can write
T = (2/(αb))·(2m/E)¹⸍²·b/(1+b²)¹⸍²·arctan[ tanξ·(1+b²)¹⸍² / b ] | {tanξ;1;∞} =
= (2/(α))·(2m/E)¹⸍²/(1+b²)¹⸍²·(π/2 - 0) =
= (π/(α))·(2m/E)¹⸍²/(1+U₀/E)¹⸍² =
= (π/(α))·(2m/(E+U₀))¹⸍² = T,
which is our final result.
Here it is easy to think that every integral is a world in its own. Integration is an art. Differentiation is mechanical and easy. It is like multiplication of two prime numbers: easy and direct. But once you have the product, how to find the factors? Very complicated.
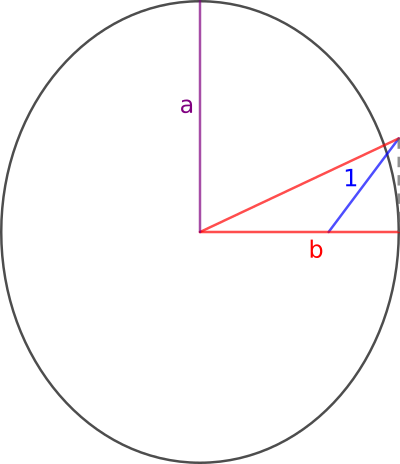
The first form of the integral had (1 - something²)¹⸍² in the denominator. It is always a good idea to try to force this "something" to be either a sine or a cosine, so that the square root will be converted into a cosine or a sine. The change of variables is sinξ=btanϕ (ϕ=αx), which has a geometric significance, as we can see in the figure:
./|
(b²+sin²ξ)¹⸍².'/ |
↘ .' / |
.' / |
.' /1 | sinξ
.' / |
.' ϕ / ξ |
.'_\____/_\_____|
--cosξ---
-------b---------
From sinξ=btanϕ we clearly develop
dξ·cosξ = b·dϕ/cos²ϕ => => cos²ϕ·dξ = b·dϕ / cosξ.
How strange is the last movement! It seems to mix the variables. But see from the figure that
cos²ϕ = b²/(b²+sin²ξ) cosξ = (1 - b²tan²ϕ)¹⸍².
Then, we get
b²·dξ / (b²+sin²ξ) = b·dϕ / (1 - b²tan²ϕ)¹⸍²,
which is the change we have performed.
What about the second trick? Is it a purely algebraic manipulation or does it have a geometric significance as well?
Notice we have written
b² + sin²ϕ = (bcosξ)² + (1+b²)sin²ξ,
and, if we define
X = b·cosξ Y = (1+b²)1+b²)¹⸍²·sinξ ≡ a·sinξ,
we get the parametric equation of an ellipse,
(X,Y) = (b·cosξ, a·sinξ)
or just
X²/b² + Y²/a² = 1.
This is an ellipse with b as horizontal semi-minor axis and with a as vertical semi-major axis.
See how the expression b² + sin²ξ is just X² + Y², or in other words, the distance from the centre of the ellipse to a point in the ellipse.
The parameter ξ is the eccentric anomaly of the ellipse, which is NOT the angle of the vector (X,Y).
In the following picture we describe the geometric significance of what we have done here.
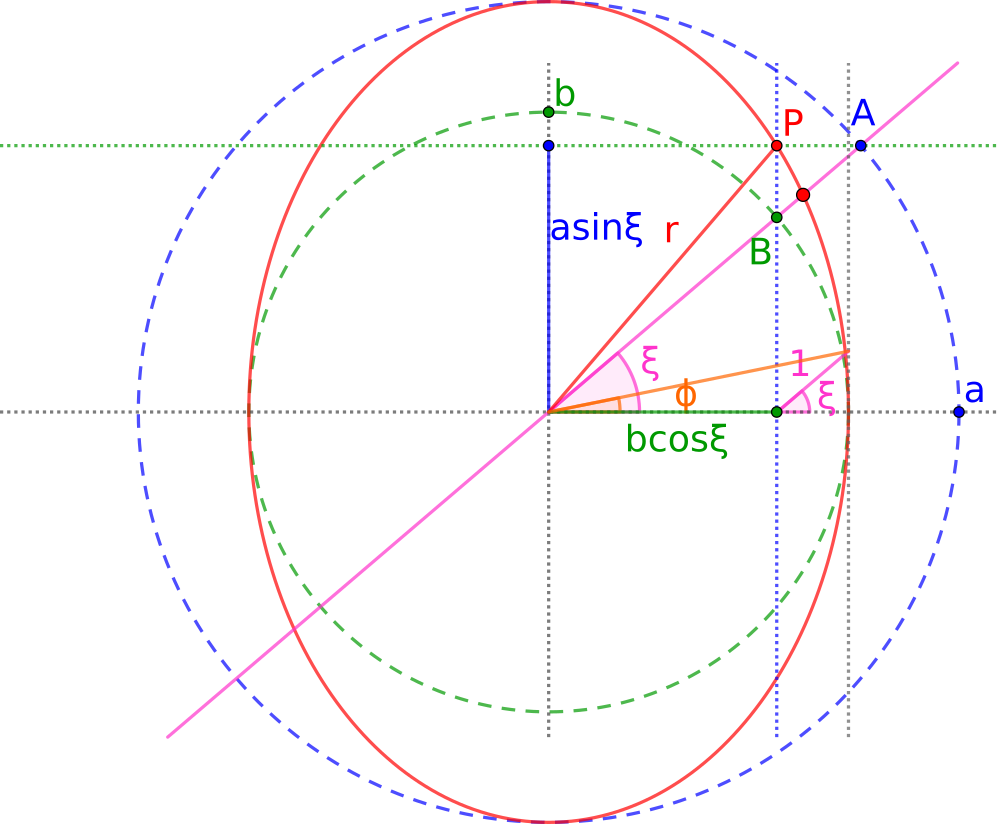
In pink you can see the original segment of length 1 with angle ξ.
In orange you can see the segment with angle ϕ, which has b as horizontal projection.
Once we have b, we draw the green dashed circle with radius b.
Since we want a²=1+b², we can draw the corresponding circle with radius a, in dashed blue.
The ellipse is formed by these two parameters, a and b. It is drawn in red.
Since we know ξ, we draw a ray from the centre of the ellipse, also in pink, following the same angle ξ. It cuts the circles in points A and B.
We can be tempted to think that the cut of this ray on the ellipse is our point of the ellipse. This would be incorrect, and we would mistakenly think that ξ is the angle of the position vector.
But the true position on the ellipse is P, and it can be taken from points A and B if we form a right-angled triangle with sides that are horizontal and vertical. The intersection of these sides is point P, which has a position vector with an angle that is not ξ in general.
In summary, if we want to understand the geometric significance of the changes we have done in the integral, first we begin with the orange segment with angle ϕ, from which we build the little pink one, with angle ξ.
Then, from the little pink and from quantity b we build a²=1+b² and then we have the parameters of a vertical ellipse. Its centre is at the left corner of our initial horizontal segment.
We see how the expression b² + sin²ξ is nothing but r², where r is the position radius (its magnitude) drawn in red in the book. This red r is our denominator, but we don't integrate over r because ellipses are better parametrised with the eccentric anomaly, which happens to be the angle ξ again, now drawn as the big pink segment.
The integral runs from ξ=0, which renders a horizontal position to the right side (here ξ describes the angle of the position vector), up to sinξ=1, which corresponds to ξ=π/2.
But in order to find the period we multiply the result by 4, which means that we cover the whole length of the ellipse.
Our last step should be to interpret what is T in terms of the geometry of this ellipse.
If we look at the picture, we can see that the red segment (r), has a mysterious angle that we can call φ. From the picture, it is clear that
tanφ = (a·sinξ) / (b·cosξ) = (a/b)·tanξ.
Then, we recover a familiar expression
φ = arctan[(a/b)·tanξ].
This is exactly the result of our integral, up to a prefactor a/b,
∫ b²·dξ / (b² + sin²ξ) = (a/b)·φ.
This is the profound meaning that we were looking for in this integral. What we obtained, up to prefactors, is the angle of the vector position of the ellipse. In other words,
∫ b²·dξ / r² = (a/b)·φ.
The integral was just to consider that a whole revolution is an angle 2π !
Another way to write this useful result is
∫ dξ / (cos²ξ + (a/b)²sin²ξ) = (a/b)·φ.