From the isotropy of space, the mechanical properties of a system cannot be different if we rotate it in space. We consider an infinitesimal rotation for now, but the system cannot change by any finite rotation either.
In 3d, we can use a vector to specify an infinitesimal rotation. Let's call it |δϕ>. Its magnitude is δϕ, the total rotated angle, and its direction is that of the axis of rotation. An axis has two possible directions, but we take the sign convention of the right hand, so that the right thumb indicates the direction when the other four fingers indicate the arc of the rotation.
So, if we have a vector position |r>, how is it affected by such rotation? First of all consider that this vector position has its origin on the rotation axis. Let's draw a picture to clarify this setup, in which we choose the rotation axis to be vertical, without losing generality,
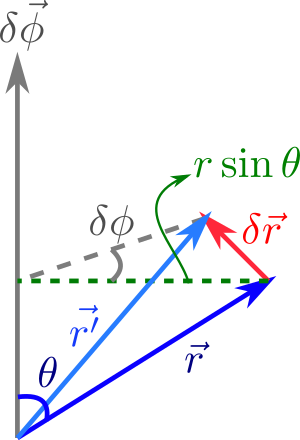
If the transformation converts |r> into |r'>, we can see that |r'> = |r> + |δr>. Now, consider the angle δϕ as small, although in the figure it has been exaggerated. Consider as well the green dashed line as r⟂ = rsinθ. Then, consider |δr> as a small arc with radius r⟂ abd angle δϕ. This is only true for a very small δϕ. We can write
||δr>| = r⟂·δϕ = r·δϕ·sinθ.
Notice how θ is the angle between |r> and |δϕ>, so that we get the product of the magnitudes of these two vector times the sine of the angle between them. This is the signature of a cross product:
The magnitude of |a> ⨯ |b> is a·b·sinα where α is the angle between the two vectors.
Conclusion, we can write the vector equation:
|δr> = |δϕ> ⨯ |r>.
This is a very important equation in mechanics for 3d rotations. For every vector |a> that has its base at the axis of rotation, the vector increment is |δa> = |δϕ> ⨯ |r> and the final vector is |a'> = |a> + |δa>. We can apply it to the velocity as well, so |δv> = |δϕ> ⨯ |v>. And also to acceleration, if we want.
If we expand again the variation for a Lagrangian, we recall that
δL = ∑( (∂L/∂|rₐ>)·δ|rₐ> + (∂L/∂|vₐ>)·δ|vₐ> ) = 0.
We already know that ∂L/∂|vₐ> = |pₐ>, and that ∂L/∂|rₐ> = |ṗₐ>. We can plug these expressions in the previous expansions of L, also plugging the expressions just found for |δrₐ> and |δvₐ>. We get
δL = ∑( |ṗₐ>·[|δϕ>⨯|rₐ>] + |pₐ>·[|δϕ>⨯|vₐ>] ) .
Now we use the triple scalar product rule:
<a|·(|b>⨯|c>) = <b|·(|c>⨯|a>) = <c|·(|a>⨯|b>).
This rule is easy to memorise as the letters a,b,c always go in cyclical+alphabetical order. The three equal quantities above represent the volume of the parallelepiped formed by the sides |a>, |b> and |c>.
We apply this rule to both terms in δL, so that |δϕ> always comes first:
|ṗₐ> · ( |δϕ> ⨯ |rₐ> ) = |δϕ> · ( |rₐ> ⨯ |ṗₐ> ) |pₐ> · ( |δϕ> ⨯ |vₐ> ) = |δϕ> · ( |vₐ> ⨯ |pₐ> ) .
Then we write again δL as
δL = 1δϕ> · ∑( |rₐ>⨯|ṗₐ> + |vₐ>⨯|pₐ> ) = |δϕ>·(d/dt)∑|rₐ>⨯|pₐ> = 0.
As |δϕ> is arbitrary, the above expression is only correct if
∑ |rₐ> ⨯ |pₐ> = |constant> ≡ |M> = angular momentum,
also called moment of momentum. The expression moment of (whatever) is used for |r> ⨯ |whatever>. We have the moment of force, moment of momentum and so on.
Conclusion: angular momentum |M> is constant in a closed system. Like (linear) momentum (you can call |p> momentum or linear momentum), |M> is additive, whether the constituents particles interact or not.
Now you may think: we have energy, momentum and angular momentum as additive integrals of motion. How many more are there? The answer is that these three are the only ones. For each closed system there are seven quantities that are additive integrals of motion: three components of |p>, three components of |M> and E.
There are many more integrals of motion, but they will not be additive. And we need the additive property in order to make useful conservation relations.
Angular momentum is trickier than momentum or energy. Since it needs the radius vectors of the particles, the value of |M> depends on the choice of origin. Also, keep in mind that our calculations are for radius vectors with base at the axis of rotation.
If we translate our origin so that |rₐ> = |r'ₐ> + |a>,
|M> = ∑|rₐ>⨯|pₐ> = ∑|r'ₐ>⨯|pₐ> + ∑|a>⨯|pₐ> = |M'> + |a>⨯|P>.
An interesting thing here is that if the system is at rest as a whole, |P> = |0>, and then |M>=|M'>, so the momentum does not depend on the choice of origin.
We can also change our frame of reference between our usual K and K', which move with a relative velocity |V>.
We suppose that the radius vectors are the same for K and K' at a given instant. And we know that |vₐ> = |v'ₐ> + |V>, so
|M> = ∑mₐ|rₐ>⨯|vₐ> = ∑mₐ|rₐ>⨯|v'ₐ> + ∑mₐ|rₐ>⨯|V>.
The first term is just |M'>, the angular momentum in frame K'. Don't confuse this |M'> with the previous |M'> in which we only translated the origin, not the frame.
The second term is μ|R>⨯|V>, so we get
|M> = |M'> + μ|R> ⨯ |V>.
For the particular case in which the whole system is at rest in K', then don't be tempted to do |M'> = |0>, since a system at rest can have angular momentum. But in this case, μ|V> = |P>, so we can write
|M> = |M'> + |R> ⨯ |P>.
This expression is of great importance. On the right hand side of the equation, the first term is the *intrinsic angular momentum* or *spin*. The second term is the angular momentum due to the motion of the whole system. This separation is of paramount relevance in Quantum Mechanics.
The conservation of angular momentum is valid for closed systems. But, as happened with momentum, we can have restricted forms of conservation for special cases of an external field.
If the field is symmetrical wrt the *axis* of rotation, such direction does not appear in the Lagrangian, and then the projection of |M> along such axis will be conserved. In particular, if the field is symmetric about an axis parallel to x, then Mx is conserved.
We recall again that the radius vectors, and hence the angular momentum, must be defined relative to an origin on the axis.
The most important particular case in physics is that of a central field (or centrally symmetric field). In such a field, the potential energy depends only on the distance from a particular point, called the centre of the field.
In a central field, we are not having a field which is symmetric about an axis, but about a point, the centre. This means that this field is symmetric about *all* axes passing through that point. So, if we take |M> relative to such point, |M> will be conserved along *all* directions. In other words, it will completely conserved. In summary: if we have a central field, take its centre as the reference point for radius vectors and then |M> will be conserved.
If we have an homogeneous field in the z direction, meaning that the field does not change if we move along z (but it can change if we move along xy), then the coordinate z cannot appear in U, and then the z component of angular momentum is conserved. This is valid for all points of reference.
The projection of angular momentum along a given axis can be found by differentiation. For example, for the z axis we have
Mz = ∑∂L/∂[ϕₐ·],
where ϕ is the rotation angle around that axis. In cylindrical coordinates r,ϕ,z we have xₐ=rₐcosϕₐ and yₐ=rₐsinϕₐ. We also know that Mz = ∑xₐ·pₐ_y - yₐ·pₐ_x = ∑mₐ(xₐẏₐ - yₐẋₐ) = ∑mₐrₐ²[ϕₐ·]. If we write the Lagrangian in cylindrical coordinates,
L = ∑(mₐ/2) · (ṙₐ² + rₐ²[ϕₐ·]² + żₐ²) - U,
and differentiate wrt [ϕₐ·], we can complete the proof.
Compare this result, Mz = ∂L/∂[ϕ·], to pz = ∂L/∂ż.
Write the magnitude of |M> and its Cartesian components as a function of the cylindrical coordinates.
Since x=rcosϕ, y=rsinϕ and z=z, and since
| î ĵ k̂ | ( yż - zẏ )
| | ( )
|M> = m·| x y z | = m·( zẋ - xż ) ,
| | ( )
| ẋ ẏ ż | ( xẏ - yẋ )
we can write
Mx = m·(żrsinϕ - zṙsinϕ - zr[ϕ·]cosϕ). My = m·(zṙcosϕ - zr[ϕ·]sinϕ - żrcosϕ). Mz = mr²[ϕ·]. M² = m²r²[ϕ·]²·(r²+z²) + m²·(rż-zṙ)².
See how M² does not depend on ϕ, as expected.
Repeat the process of spherical coordinates.
x = r·cosϕsinθ y = r·sinϕsinθ z = r·cosθ.
Then we can write, always extracting r² as prefactor,
Mx = -m·r²·([θ·]sinϕ + [ϕ·]cosϕsinθcosθ). My = m·r²·([θ·]cosϕ - [ϕ·]cosθsinϕsinθ). Mz = m·r²·([ϕ·]sin²θ). M² = m²·r⁴·([θ·]² + [ϕ·]²sin²θ).
Again, M² cannot depend on θ or ϕ.
For each field, which components of |P> and |M> are conserved?
a) A field homogeneous in the plane xy. This means that the field does not change when changing xy.
The coordinates x and y cannot appear in the Lagrangian, so Px and Py are conserved. Since Px and Py are both involved in Mz, Mz it is also conserved. We can also say that a rotation about z involves motion in the xy plane, which will not change the field.
b) A field homogeneous in a cylinder. This means that the field does not change if we move on a cylinder.
The coordinate z will not affect anything, so Pz is conserved. A rotation about the z axis does not affect either, so Mz is also conserved.
c) A field homogeneous in a prism, with edges parallel to the z axis.
A prism is a 3d figure with a polygon as a base and then a column with the polygon shape raised above it.
Since moving along z does not change anything, Pz is conserved. No component of |M> can be conserved here. And if we rotate a finite angle corresponding to the polygon shape?
d) Two points joined by the z axis.
In this case, no |P> component is conserved. For the angular momentum, rotating about z does not change anything, so Mz is conserved.
e) Infinite homogeneous half-plane xy in which the edge is along x.
Px will be conserved.
f) Homogeneous cone with z axis as symmetry axis.
Clearly, Mz is the quantity conserved.
g) Homogeneous circular torus with z as symmetry axis.
Here, Mz is conserved.
h) Infinite homogeneous cylindrical helix along z.
Nothing can be conserved here. Although if we couple a rotation δϕ about z with a translation δz = hδϕ/(2π) along z [h is the pitch of the helix here], the field is maintained constant.
This means that δL = δz(∂L/∂z) + δϕ(∂L/∂ϕ) = 0, which implies δz·Ṗz + δϕ·Ṁz = 0, and then δϕ·(h·Ṗz/(2π) + Ṁz) = 0. This implies that Mz + h·Pz/(2π) = constant.